INTRODUCTION
Many pharmaceutically important processes like synthesis, extraction, recrystallization, purification, and dosage form development require the solubilization of an active pharmaceutical ingredient (API) in neat and/or solvent blends. Many times these APIs are complex organic substances and are ideal theoretical candidates for understanding solubility behavior with the use of predictive methods. Itraconazole (ITRA) (Figure 1) is one such triazole compound widely used because of its antifungal activity. However, its use is limited due to its poor solubility.1,2 Knowledge about its solubility behavior and solubility improvement is much needed for the development of better formulations with increased effectiveness. Thus, ITRA is an ideal candidate for estimating its solubility and understanding its solubility behavior in solvent mixtures with the help of empirical predictive models.
The Hildebrand-Scatchard equation is an empirical approach used to predict the solubility of poorly soluble compounds in a variety of solvents ranging from nonpolar to polar according to regular solution theory.3 However, in pharmaceuticals many irregular solutions are observed due to self-association of solute or solvent molecules and complexation.
The extended Hildebrand solubility approach (EHSA) is an adaptation of the Hildebrand-Scatchard equation that allows the estimation of solubilities of polar as well as nonpolar moieties in a variety of solvents with different polarities like water, alcohols, sulfoxides, glycols, and acetates.4 The EHSA has been considered as an adventitious empirical model for prediction of solubility due to numerous reasons. They include ability of solubility prediction of a wide variety of solutes in irregular solutions, ability of predicting the solubility of any solute in pure or mixed solvents using fundamental physicochemical properties, it is applicable not only for crystalline solids in liquid solutions but also for liquid-liquid and gas-liquid systems, and it gives more accurate prediction of mole fraction solubilities compared to other empirical methods. The solubility parameter, an intrinsic physicochemical property of solute and solvent, is the square root of cohesive energy density and could be used to understand the solution behavior of regular and irregular solutions. To date, some work has been done to study the solubility behavior of pharmaceutically important substances with the use of EHSA by Martin et al.,5 Bustamante et al.,6 Rathi and Mourya,7 Sotomayor et al.,8 and Delgado et al.9
The solubility of crystalline solids in a variety of solutions can be described with the EHSA expression as5
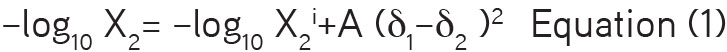
The solubility of crystalline solid solute in irregular solutions may be estimated using the following equation:10
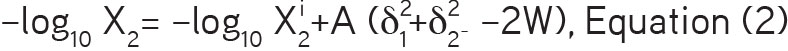
Where are the ideal mole fraction and experimental mole fraction solubility of the solute, respectively. The terms and are the solubility parameters of the respective solvent mixtures and the solute, respectively. Furthermore, represents the interaction energy parameter for the solute-solvent blend interaction in irregular solutions.
The term in Equations 1 and 2 can be expressed as
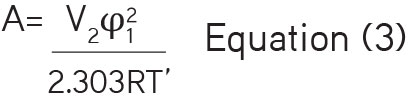
where V2 represents the molar volume of the solute, i.e. ITRA, R represents universal gas constant, and φ1 expresses the volume fraction of the solvent mixture.
The volume fraction φ1 can be calculated as
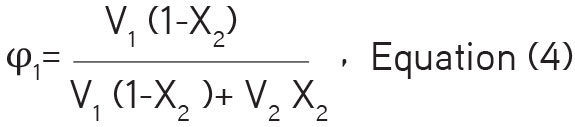
where V1 is the reflected molar volume of the triacetin: water solvent mixture. X1 and X2 represent moles of the solute and solvent, respectively.
The ideal mole fraction solubility can be expressed as a negative logarithm and can be given by the following equation:
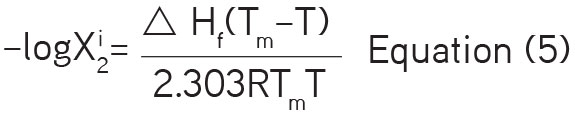
Here ΔHf gives fusion enthalpy of solid crystalline ITRA. Tm reflects melting temperature and represents the absolute temperature (298.15 K).
The logarithmic value of the activity coefficient could be expressed by the equation
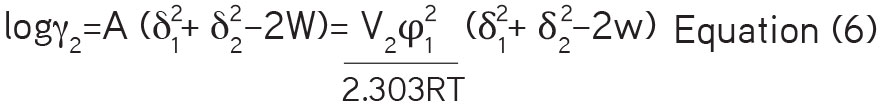
As we could not confine the interaction term W, the other approach will be an experimental estimation of interaction energy by determining ITRA solubility in solvent mixtures using Equation 2. A realistic equation for the determination of W has not been reported to date. Hence, it is evaluated using Equation 6 by back calculations. Then these values of W can be used further for the prediction of the solubility of a solute in any other solvent system as a function of the solubility parameter of the respective solvent mixture.

Triacetin is a pharmaceutically important chemical substance used as a solvent11 for the solubilization of various drugs and polymers because of its biocompatibility in topical and injectable preparations.12,13 It is also capable of affecting the film-forming properties14 as well as adhesive properties in topical preparations and is capable of forming stable depots in the case of injectable preparations.15
Thus, the present work was carried out to establish the suitability of EHSA to study the solute-solvent interaction and solution behavior and to predict the solubility of ITRA in triacetin: water mixtures as a function of the solubility parameter.
MATERIALS AND METHODS
Materials
A gift sample of ITRA was obtained from USV (Mumbai, India). The solvents like triacetin were received from Loba Chemie (India). The double distilled water used in the study was prepared in the laboratory. Other chemicals and reagents used in the study were of analytical grade.
Determination of itraconazole solubility
The saturation solubility study method was employed for the determination of ITRA solubility.16 Double distilled water was used to prepare solvent mixtures. Binary compositions of triacetin: water were used from 0% to 100% by the mass fraction of triacetin. Then 10 g of binary solvents blends were taken in screw cap vials and were saturated by the addition of excess of drug. These vials were mounted in an orbital shaker (Remi, India) at 298.15 K and 100 rpm for 72 h. The saturation time of 72 h was established through the preliminary studies. After 72 h, these vials were removed and the solutions were filtered carefully with the help of micro filters of 0.45 µm. The filtrate was collected, diluted suitably, and was subjected to spectrophotometric analysis using a double beam ultraviolet spectrophotometer (Shimadzu, Japan) at 255 nm. All the experiments were performed in triplicate. The densities of pure solvent blends and filtered saturated blends were determined and used for the estimation of saturated solubilities in terms of mole fraction.
Differential scanning calorimetric (DSC) study
The melting temperature and melting fusion enthalpy of ITRA were determined by performing DSC analysis. The DSC thermogram was produced using a differential scanning calorimeter (DSC-1, Mettler Toledo, Switzerland). An ITRA sample weighing 5.0 mg was kept in an aluminum pan and then it was sealed with the lid. These pans were subjected to heating from 313.15 K to 573.154 K at a rate of 10 K.min-1 under nitrogen purging.
Statistical analysis
Statistical analysis of the solubility data was performed using the EHSA. The polynomial regression analysis and statistical evaluation of the data were performed using Minitab statistical software (Version 18) and MS Excel.
RESULTS AND DISCUSSION
The melting temperature (Tm) of ITRA was 443.5 K and the melting fusion enthalpy ( was 65.32 kJ.moL-1 at 298.15 K. From these values, the ideal mole fraction solubility of the drug was estimated to be and the value of was found to be 3.04 expressed in mole fraction using Equation 5. The investigated mole fraction solubilities of ITRA in triacetin: water mixtures with a wide range of polarity described in terms of the solubility parameter of the solvent mixture from 10.77 to 23.40 H are given in Table 1.
The uncertainties in the solubility investigation were <2% in all cases. Table 1 also expresses the mass fractions, volume fractions, and solubility parameter of the solvent blend with respect to its composition. These volume fractions and solubility parameter were determined using the additive property phenomenon. The solubilities of ITRA in terms of molarity and mole fractions are also presented in Table 1.
The ideal, experimental, and calculated solubilities of ITRA with respect to the solubility parameter of the solvent blend for regular solutions at 298.15 K are presented in Figure 2. These calculated solubilities were estimated using molar volume and solubility parameters. The values were obtained from the literature for solvents. For ITRA, these values were calculated using Fedors’ group contribution method.17 According to regular solutions theory, the peak in solubility would be attained where the solubility parameter of the solvent mixture matches that of the solute (Figure 2). In the present study, it was observed that the peak in solubility of ITRA was achieved in a solvent blend of 0.9 mass fractions of triacetin where the solubility parameter of ITRA nearly corresponded with that of the solvent mixture (δ1=12.03 H). This was attributed to the matching of polarities of ITRA and 0.9 mass fraction of solvent mixture of triacetin: water. From the results it could be inferred that the ITRA has the same polarity as that of the 0.9 mass fraction of the solvent mixture of triacetin: water. The molar volume and solubility parameter of ITRA were derived using Fedors’ contribution method and were found to be 457.5 cm3.mol-1 and 24.3987 (J/cm3)1/2 or 11.93 H, respectively.
Volume fractions (φ1) of the solvent mixtures were estimated using Equation 4. The values were nearly equal to unity due to the smaller values of solubility of ITRA in all the solvent mixtures. The values of activity coefficients are also given in Table 1. These values were greater than one in solvent mixtures where the proportion of water was higher. Table 2 summarizes experimental parameters like volume fractions of solvent mixture (∅1), A, K, Wobs, Wcal and ITRA in triacetin: water mixtures at 298.15 K. It was observed that the values of the Walker parameter were greater than one, indicating a rise in solubilities due to increased solute-solvent interactions. The variation in interaction energy parameter W with respect to the solubility parameter of the solvent blend is shown in Figure 3. The graph shows the deviation from linearity as the value of W was estimated using the squares of two terms (δ1 and δ2) and a variable term consisting of (-log10γ2/A) as reflected in following equation:
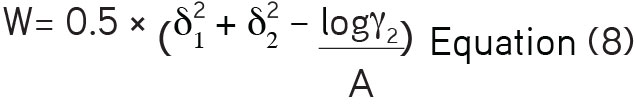
The values of were estimated using a regular polynomial equation as a function of solubility parameter of solvent blend in order 5 (Equation 7). The following polynomial regression equation of order 5 was produced as a function of the solubility parameter to back calculate the values of :
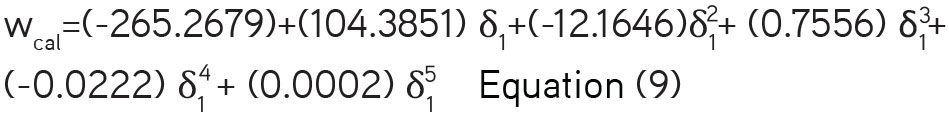
These back calculated values of Wcal were used to calculate the solubilities of ITRA (Table 3). Such theoretically estimated solubilities were then compared with experimental ones and the mean percent deviation was obtained. It was found to be 9.76% for the EHSA method. The worth of the EHSA method for the correlation and estimation of solubilities with the use of the EHSA equation could be established by performing the calculations using an equation consisting of other variables. Therefore, the theoretical solubility values were calculated using the direct method based upon polynomial equation of log10X2 as a function of the solubility parameter of solvent blend δ1 of order 5 (Equation 10).
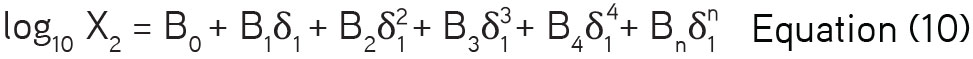
Here calculated solubilities were again compared with experimental ones and the mean percent deviation was obtained. It was -1.89% (Table 3). The solubility prediction capabilities of both methods were compared using these mean percent deviation values. Similarly, solubility prediction behavior was obtained with the use of polynomial regression equations of order 5 for EHSA and the direct method for drugs like phenacetin,18 meloxicam,19 and piroxicam.8 In the present study, the solubility correlation and prediction were better by the direct method as compared to that of EHSA with a polynomial of order 5. Nonetheless, it must be remembered that these methods were based upon some of the physico-chemical properties. There is a need for a method for the exact determination of the Walker parameter for the estimation of interaction energy parameter. Already it has been proved that the EHSA method could be used to calculate drug solubilities as it depended upon some simpler physicochemical properties like solubility parameter, molar volume, and experimental solubilities. Thus, EHSA could have potential applications in various pharmaceutical science processes.
ITRA showed both positive and negative deviations in solubility as reported previously (Figure 4).20,21 The reason for such deviation from ideal solubilization could be the predominance of interactions between cosolvent and water over the solute-solvent interactions.22 Similar types of observations were reported by Gómez et al.,23 Kharwade et al.,24 Thimmasetty et al.,25 Rathi and Deshpande,26 and Cárdenas et al.27 The major force behind the solubilization in water-rich mixtures could be entropy. It might have resulted in loss in structure of water surrounding the nonpolar ITRA by triacetin molecules. At the higher proportions of triacetin, the solubilization could be enthalpy driven. At these higher proportions of triacetin water molecules might have lost their three dimensional structure completely and they might have become available for interaction with ITRA molecules.19 The other reason for the positive deviation from the log linear model could be the drug-drug molecule interactions in the saturated solution. This could be further confirmed with spectral studies.
CONCLUSION
The present study showed the application of EHSA to the ITRA solubility data in triacetin: water mixtures at 298.15 K with the help of physicochemical properties like fusion enthalpy, molar volume, and Hildebrand solubility parameter obtained by Fedors’ group contribution method. The peak in experimental solubility was observed at a point where the solubility parameter of ITRA matched that of the solvent mixture. Better prediction of solubilities was achieved with the help of a polynomial regression equation as a function of the solubility parameter of order 5 for both EHSA and the direct method. The direct method exhibited better prediction capacities (mean percent deviations -1.89%) as compared to EHSA (mean percent deviations 9.76%). Furthermore, it could be asserted based on the study that EHSA should be used to understand the solubility behavior of solutes of different polarities in a variety of solvents and their mixtures. The information obtained could be useful for the process and formulation development of such drugs.
ACKNOWLEDGEMENT
The authors are grateful to Marathwada Mitramandal’s College of Pharmacy, Kalewadi-Pune, India and Y B Chavan College of Pharmacy, Aurangabad, India for providing the necessary facilities to carry out the study.
Conflict of Interest: No conflict of interest was declared by the authors.