INTRODUCTION
Boric acid is a weak acid that forms a white and water-soluble powder.1 It can be naturally found in seawater, many plants, and most fruits. Boric acid has been used as a mild antiseptic or bacteriostat in eyewashes and mouthwashes. Aqueous solutions of boric acid are topically used for ophthalmic irrigation to cleanse, refresh, and soothe irritated eyes and used for removal of loose foreign material, air pollutants, or chlorinated water.2
Boric acid is predominantly eliminated unchanged by the kidney; small amounts are also excreted in sweat, salvia, and feces. Boric acid is concentrated in the brain and liver.3 Boric acid and its derivatives have been shown to promote riboflavinuria in both animals and humans.4
Metabolism of inorganic borates by biological systems is not feasible because excessive energy is required to break the boron-oxygen bond. Inorganic borates, in low concentrations, convert to boric acid at physiological pH in the aqueous layer overlying mucosal surfaces prior to absorption.5
Studies of the acidity of organic compounds are important and play a very significant role in the evaluation of the activity, reaction mechanisms, and structures of organic compounds.
Equilibrium constants for ionization reactions are usually called ionization constants or acidic dissociation constants (pKa). pKa is an important physico-chemical parameter in drug absorption. Many drug compounds include at least one acid and/or basic group, and the ionization state of these groups plays an important role in determining the physico-chemical properties of compounds. Information about the pKa value of compounds plays a major role in the expansion of drug formulations.6,7,8
Reliable and accurate methods for calculating relative and absolute pKa values are important for understanding of the effective pKa values in molecules. Some studies detailing the acid-base properties of compounds in aqueous solutions and in the gas phase are also available.9 Different experimental procedures are frequently used for the determination of acidity constants. These methods are high-pressure liquid chromatography, liquid-liquid partitioning chromatography, and methods that involve potentiometric titrations or spectrophotometric determination in water or in mixtures of solvents. Manov et al.10 determined the ionization constant of boric acid and the pH of certain borax-chloride buffer solutions from 0 to 60°C. Arcis et al.11 determined the ionization of boric acid in water from 298 K to 623 K by AC conductivity and Raman spectroscopy. Dickson carried out emf measurements using the cell: Pt | H2 (g, 101.325 kPa) | borax in synthetic seawater | AgCl; Ag over the temperature range 273.15-318.15 K, and at five salinities from 5 to 45. The obtained results of that research work were used to calculate the stoichiometric (ionic medium) dissociation constant for boric acid in seawater media on the “total” hydrogen ion scale.12
For boric acid, the values of pKa can be calculated using ab initio and density functional theory (DFT) methods.13,14,15,16,17,18 These computational methods have an important advantage. In these methods, the important structural properties of molecules, in solution, such as the dihedral angle between the indicated atoms (D); total atomic charge (Mulliken) (q); bond lengths between the indicated atoms (d); and bond angles (A) are calculated. These structural properties can be used in research works as well as in various industries.
In the DFT method, the calculation of electronic structure was performed with DFT and the electrostatic features were modeled through external charge distributions and continuum dielectrics. The polarizable continuum model (PCM) using the integral equation formalism variant PCM is the default self-consistent reaction field (SCRF) method. This method creates the solute cavity via a set of overlapping spheres. It was initially devised by Tomasi and coworkers and Pascual-Ahuir and coworkers. Tomasi’s method allowed us to prove that cations, neutral molecules, and anions form intermolecular hydrogen bonds (IHBs) with some molecules of water.19
The present paper deals with the influence of factors such as the SCRF model applied, choice of a particular thermodynamic equation, atomic radii used to build a cavity in the solvent (water), optimization of geometry in water, inclusion of electron correlation, and the dimension of the basis set on the solvation free energies and on the calculated pKa values. The pKa value of boric acid was calculated in aqueous solution by ab initio and DFT methods and temperature of 25°C. We investigated the molecular conformations and solute-solvent interactions of the cation, anion, and neutral species of boric acid to explain the obtained acidic dissociation constants.
MATERIALS AND METHODS
Initially, the structure of species of boric acid was optimized by semiempirical PM3 method in the program HyperChem (CS Chem 3D version 5.0). All calculations about the geometries of the initial and solvated molecules in water were done using the software package Gaussian 09. The DFT calculations were carried out using the hybrid exchange-correlation functional of Becke, Lee, Yang, and Parr (B3LYP) and the Gaussian 6-31G (d) basis set was used.20
To analyze the solvent effects on all species involved in the selected ionization reaction, the PCM of Miertus and Tomasi.21 was used. In this method, the solvent is represented as a structureless polarizable medium characterized by its dielectric constant. Finally, we selected the solvation of the species by means of IHBS that involve one molecule of the mentioned species and some molecules of water.
RESULTS AND DISCUSSION
The trend of a molecule to lose its H+ is quantified as pKa. Boric acid is a weak acid and it has three acid groups. A proton can separate from the hydroxyl group to give an ionized species (Figure 1). This concept of microscopic ionization constant is shown in Equation 1:
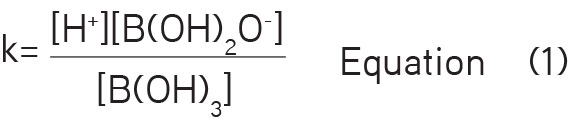
The total free energies (in Hartree and kJ.mol-1) for the single and solvated species of boric acid, in water, were calculated at the B3LYP/6-31+G (d) level of the theory, using Tomasi’s method, at T=298.15 K and the results are shown in Table 1. This table shows that the total free energy for various species of boric acid increases with increasing number of water molecules. It shows that the solvation process causes an increase in the total free energy for various species of boric acid. In other words, solvation of the boric acid is an endothermic process. The values of total free energy for various species of boric acid (Table 1) were applied to calculate the pKa value of boric acid. In addition, these data help us to suggest an appropriate reaction regarding the deprotonation process of boric acid.
Various reactions including the neutral and anion species of boric acid were considered in the program Excel and some of these reactions were not considered further because their equilibrium constants were not comparable with the experimental ones. The selected equation for the deprotonation process of boric acid as well as the experimentally determined and theoretically calculated pKa is shown in Table 2.
Ionization constant of boric acid
In aqueous solutions, the molecule of boric acid can undergo the below reaction:
H3L(H2O)4+OH-⇆H2L-(H2O)3+2H2O Kc Equation (2)
In the above reaction, H3L(H2O)4 (Figure 2A) is the neutral species of boric acid solvated with four molecules of water and H2L-(H2O)3 (Figure 2B) represents the anion species of boric acid solvated with three water molecules.
During the reaction of Equation 2, the autopyrolysis of two water molecules, in pure water, can occur as shown below:
2H2O ⇆ OH–+H3O+ Kw=1.008×10-14 Equation (3)
The very low amount of Kw shows that a few water molecules are ionized in pure liquid water.
The reaction of Equation 4 can be obtained by combining Equation 2 and 3:
H3L(H2O)4 ⇆ H2L-(H2O)3+H3O+ Ka Equation (4)
It is clear that the value of Ka can be calculated using Kc and Kw as below:
Ka=Kc×Kw Equation (5)
Equation 5 was applied to calculate the values of the ionization constant of boric acid, Ka, in water at T=298.15 K. The theoretically calculated value of pKa for boric acid at T=298.15 K is shown in Table 2. As can be seen in this table, there is good agreement between the experimentally determined (pKa=9.237)22 and theoretically calculated pKa values of boric acid at this temperature.
Table 3 shows the optimized values of structural properties for the anion and neutral species of boric acid, in water, obtained at the B3LYP/6-31+G (d) level of theory with Tomasi’s method at T=298.15 K.
As can be seen in Table 3, for boric acid, the values of qO4 for HL-(H2O)3 and H2L(H2O)4 are -1.104481 and -0.907847, respectively. It shows that the absolute value of electrical charge around the O4 atom in HL-(H2O)3, compared to that in H2L(H2O)4, increases and it can imply H+ separates from the O4 atom during the deprotonation process of boric acid in water.
Study on H-bonding between selected species of boric acid and water
The structural properties of a species, solved in water, can help us to understand the interaction between this species and water (H-bonding). One of the most important of these structural properties is the bond length between the indicated atoms from solute and solvent (water) molecules (in Å). These data, for neutral and cation species of boric acid, are listed in Table 3. The power of hydrogen bonds can be classified as strong (bond length is between 1.2 Å and 2.2 Å and the angle is between 175° and 180°), moderate (bond length is between 1.5 Å and 2.2 Å and the angle is between 130° and 180°), and weak (bond length is between 2.2 Å and 3.2 Å and the angle is between 90° and 150°).23 As can be seen in Table 3, for H2L(H2O)4, the bond length between atom H6, from boric acid, and O9, from water, is 2.124582 (dH6O9=2.124582). In addition, for H2L-(H2O)3, the bond length between atom O2, from boric acid, and H19, from water, is 2.098563 (dH19O2=2.098563). These data show that for boric acid the power of H-bonding between H2L(H2O)4 and water and also between H2L-(H2O)3 and water are classified as moderate. It must be noted that IHBs data can be used in the design of benefit and help us to predict nano drugs.7
CONCLUSION
In this research work, we showed the feasibility of a theoretical method, DFT and ab initio, to calculate the ionization constants of boric acid at T=298.15 K. As a result, we selected various acid-base reactions that include the solvation of the hydrogen, hydroxyl ions, and other anions or neutral molecules in protic solvents such as water, which possess a high hydrogen-bond-donor capability. The calculations performed at the B3LYP/6-31+G (d) levels of theory using Tomasi’s method allowed us to prove that neutral molecules and anions form IHBs with some molecules of water. In addition, the comparison between experimentally determined and theoretically calculated pKa, for boric acid, shows that there is good agreement between them at 298.15 K.
Conflicts of interest: No conflict of interest was declared by the authors. The authors alone are responsible for the content and writing of the paper.